二元一次方程讲解
二元一次方程讲解
二元一次方程的解法有两种,分别为:
1、代入消元法:代入消元法是将方程组中的一个方程的未知数用含有另一个未知数的代数式表示,并代入到另一个方程中去,(一定是另一个方程,不能是变形前的方程)这就消去了一个未知数,得到一个解。代入消元法简称代入法。
例如: x+y=4 ①
x-y=2 ②
由②式得出x=2+y ③
将③式代入到①式中得出 2+y+y=4
2+2y=4
2+2y-2=4-2
2y=2
y=1
x=2+y
x=3
此时,千万要注意哦!
千万别把方程组方程②式得出的③式,又代入到②式中哦。
我们是要把得到式③代到另一个方程①式中。
2、加减消元法:利用等式的性质使方程组中两个方程中的某一个未知数前的系数的绝对值相等,然后把两个方程相加或相减,以消去这个未知数,使方程只含有一个未知数而得以求解。
例如: x+2y=7 ①
2x-y=4 ②
由②式*2,即2*(2x-y)=4x2,得出4x-2y=8 ③
将①式加③式,即x+2y+4x-2y=7+8
5x=15
x=3
再把x=3代入到①式或者②式中,求出y=2。
应用题:
某体育用品商场销售A、B两款足球,售价和进价如下表:
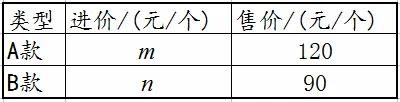
若该商场购进5个A款足球和12个B款足球需1120元;若该商场购进10个A款足球和15个B款足球需1700元。
(1)求m和n的值;
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3300元,那么该商场可获利多少元?
(3)为了提高销量,商场实施“买足球送跳绳”的促销活动:买1个A款足球送1根跳绳,买3个B款足球送2根跳绳,每根跳绳的成本为10元。某日商场售卖两款足球共盈利600元(每款都有销售),那么该日销售A、B两款足球各多少个?
解:(1) 5m+12n=1120 ①
10m+15n=1700 ②
因为两个未知数前面的系数绝对值各自不同,我们需要把一个未知数的系数通过乘法或除法变成绝对值相同的系数(因题而异) 。
这题,我们把未知数m的系数通过乘法变成绝对值相同的系数。
将①式*2得出:
(5m+12n)*2=1120*2 ③
10m+15n=1700 ④
10m+24n=2240 ⑤
10m+15n=1700 ⑥
将⑤式减去⑥式,得出10m+24n-(10m+15n) =2240-1700,求得n=60, 最后算出m=80 (元)。
(2)解题思路为下,
根据条件,列出盈利多少元的二元一次方程
(120-80)x+(90-60)y=?
简化得出40x+30y=? ①此时,一个方程两个未知数,我们是算不出结 果的。
但是,我们还有一个已知条件,并列出二元一次方程为
120x+90y=3300 ②
并且我们发现②式刚好是①式的3倍,只要我们把②式除以3就得出①式的结果了,并不用求出的x、y值。
解:(2) 120x+90y=3300 ①
将①式除以3得出40x+30y=1100(元)
解题思路为,买1个A款足球送1根跳绳,即每卖出一个A款足球盈利为(120-80)-10=30元;买3个B款足球送2根跳绳,即每卖出一个B款足球盈利为[3*(90-60)-2*10]÷3=70/3元
解:(3)假设销售A、B款足球各为x、y个。
则列方程为 30x+70y/3=600
x+7y/9=20
因为x、y必须为整数,所以y必须是9的整倍数,如9、18,其他36……不符合。得出结果为:
x=13 或 x=6
y=9 y=18








